Chapter 8 - Radioisotope Power Systems: Quantum Tunneling in Alpha Decay

Objective of the module is to study the phenomenon of radioactivity, focusing in more detail on one of the types — alpha decay. Students will be proposed to consider it in the context of quantum physics when alpha decay is interpreted as its tunneling through a potential barrier of the nucleus. Results of modeling this phenomenon based on the WKB (Wentzel-Kramers-Brillouin) approximation will then be applied to solve an applied problem at the end of the module.

Radioactive decay is the spontaneous change in the composition (atomic number $Z$, mass number $A$) or internal structure of unstable atomic nuclei through the emission of elementary particles, gamma rays, and/or nuclear fragments. This process is also referred to as radioactivity.

The next main types of radioactive decay can be distinguished:

Alpha decay — accompanied by the emission of alpha particles: the nucleus of a helium atom ($^{4}_{2}\text{He}$), consisting of 2 protons and 2 neutrons. Alpha radiation has low penetration power but high ionizing power.
Beta decay — a process in which a nucleus emits a beta particle (electron or positron). By this process, unstable atoms obtain a more stable ratio of protons to neutrons. $\beta$-radiation has greater penetration than $\alpha$-particles but moderate ionizing power
Gamma decay — accompanied by the emission of gamma quanta, that has very high penetration power.

In this module, natural radioactivity — when atoms decay spontaneously — will be considered. Most chemical elements with atomic numbers greater than 82 are unstable, and their nuclei tend to transform into more stable configurations through the emission of alpha, beta, or gamma radiation. This spontaneous process continues until a stable isotope is formed. Artificial radioactivity, on the other hand, occurs when stable nuclei are made radioactive through nuclear reactions, but it will not be discussed in detail here.

[+]

Potential Energy Profile

The profile of the radial distribution of the potential energy for electrons in an atom is presented in this section.

The total potential used for modeling $\alpha$-decay can be expressed as the sum of nuclear potentiel - $V_{WS}$ (described by Woods-Saxon potentiel), the centrifugal potential - $V_{l}$ and Coulomb potential - $V_{C}$. $$ V(r) = V_C(r) + V_l(r) + V_{WS}(r) $$ where $Z$ is the atomic number, $R$ is the nuclear radius, $V_0$ is the depth of nuclear potential well, $\sigma$ is the diffuseness parameter, $l$ and $\mu$ are the angular momentum of $\alpha$-particle and the reduced mass of the system formed by the $\alpha$-particle and the daughter nucleus, respectively.

$$ V_C(r) = \begin{cases} \frac{2(Z - 2) e^2}{2 R^3} \left[3 R^2 - r^2\right] , & r \le R, \\ \frac{2 (Z - 2)e^2}{r} , & r > R \end{cases} $$ $$ V_{WS}(r) = - \frac {V_0^{WS}} {(1 + e^{(r - R)/\sigma})}$$ $$ V_l(r) = \frac{\hbar^2 l (l + 1)} {2 \mu r^2}$$

Vertical lines that correspond to the turning points $r_1$ and $r_2$, where the potential energy $V(r)$ intersects the energy level $E^{\text{kinetic}}_{\text{initial}}$ of the $\alpha$-particle, divide the potential into three regions: inside the nucleus, the barrier (tunneling), and the free-particle region.

Numerical Energies Numerical Probabilities

Select the basic parameters for the simulation of the $\alpha$-decay for

$Z=$ , $A=$ ,

Alpha particle energy: $E^{\text{kinetic}}_{\text{initial}}=$ MeV
Alpha particle mass: $\mu=$ uma

$V_0=$ MeV, $\sigma=$ fm
The orbital number:
$l=$

Enter the number of spatial points:
$N_r=$
Enter the x-coordinates of the quantum well:
$r_0=$ fm , $r_L=$ fm

The number of eigenvalues to be displayed: $N_{eig}=$

[+]

Observable

The main parameter that characterize alpha decay are the energy of the $\alpha$-particle and the half-life $\tau_{1/2}$ in [s] which can be expressed in terms of the decay constant $\Gamma$ in [$\text{s}^{-1}$] According to the law of radioactive decay, they are related by: $$ \tau_{1/2} = \frac{\ln 2}{\Gamma} $$

As first demonstrated by Gamow, the decay constant can be expressed as $\Gamma = T/\tau $, where $T$ is the tunneling probability of the alpha particle through the potential barrier, and $\tau$ is the time between two successive collisions of the particle with the barrier. The quantity $\tau$ can be estimated from classical considerations if the nuclear radius, mass, and energy of the $\alpha$-particle are known. $$ \tau = \frac{2R}{v} \quad \text{with} \quad v = \sqrt{\frac{2E^{\text{kinetic}}_{\text{initial}}}{\mu}} $$

Thus, the problem of determining the half-life of a nucleus is equivalent to calculating the tunneling probability of the $\alpha$ particle through the potential barrier.

[+]

Gamow Approximation

The simplified potential was employed to analyze the quantum tunneling process and the decay probability of the alpha particle within Gamow's theory of $\alpha$-decay, and to obtain the corresponding wave function of the alpha particle in the following subsection.

$$ V_G(r) = \begin{cases} V_0, & r \le R, \\ \frac{2 (Z - 2)e^2}{r} , & r > R \end{cases} $$

$$ T \simeq \prod_{i=1}^{n} \exp\!\left[-\frac{2}{\hbar}\,\sqrt{2\mu\,(V_i - E)}\, dr \,\right] $$

Show segments

Parameters obtained from Gamow's approximation

[+]

WKB Approximation

For the potential presented in the Gamow approximation section, the following solutions for the wave function in different regions were obtained:

$$ \begin{cases} \psi_I(r) = Ae^{ik_1(r-r_1)} + Be^{-ik_1(r-r_1)}, & r < r_1, \\ \psi_{II}(r) = \frac{C}{\sqrt{q(r)}} e^{ -\int_{r_1}^{r_2} q(r) dr} + \frac{D}{\sqrt{q(r)}} e^{\int_{r_1}^{r_2} dr } , & r_1 <= r <= r_2 \\ \psi_{III}(r) = Fe^{ik_3(r-r_2)}, & r \gg r_2 \end{cases} $$

where $ k_1 = \frac{\sqrt{2\mu(E-V_0)}}{\hbar} $, $ k_3 = \frac{\sqrt{2\mu E}}{\hbar} $ and $q(r) = \frac{\sqrt{2\mu(V_G(r) - E)}}{\hbar}.$

$$ T = \frac{k_3|F|^2}{k_1|A|^2} = \frac{k_3}{k_1} e^{ - \frac{2}{\hbar} \int_{r_1}^{r_2} \sqrt {2 \mu [V_G(r) - E] dr} } $$ Parameters obtained from WKB (Wentzel–Kramers–Brillouin) approximation

$|\psi|^2$ $\mathrm{Re}(\psi)$

Zoom of leakage region

[+]

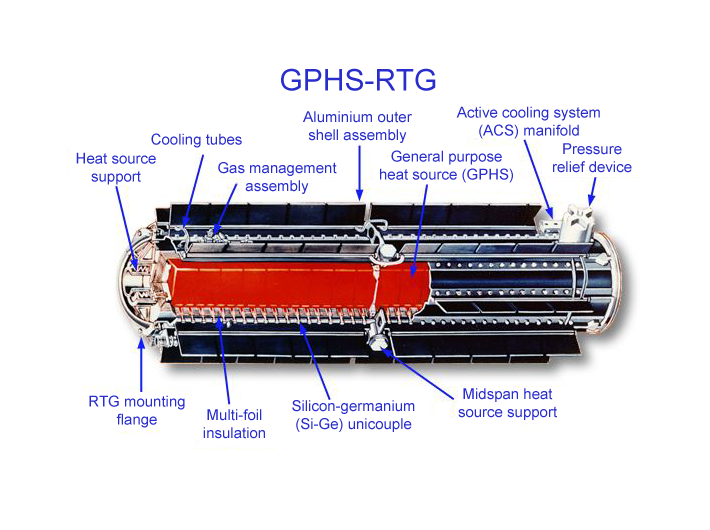
Application: Radioisotope Thermoelectric Generators

Open notebook

v.1.2 [15.06.2023-15.07.2024]. Full-stack programming and site design by M. Sosnova (mariya.v.sosnova@gmail.com)