Chapter 7 - Interference

Objective: The objective of this module is to investigate the phenomenon of interference by examining the passage of various types of waves through a double slit structure. This approach provides a deeper understanding of the phenomena of interference as well as diffraction and their interrelationship. Students will learn to calculate interference patterns using both analytical and numerical methods. Furthermore, we will explore the practical applications of interference, with a focus on using a gravimeter to determine the magnitude of the gravitational constant.

Interference (from Latin interferens is from inter - "between" and ferre - "to carry") is a phenomenon in which two coherent waves combine, taking into account their phase difference. This combination involves adding their displacements, resulting in a wave with either greater intensity (constructive interference) or reduced amplitude (destructive interference), depending on whether the waves are in phase or out of phase, respectively.

can be observed with all types of waves, for example, light, radio, acoustic, surface water waves, gravity or matter waves.

the result of interference (interference pattern) depends on the phase difference of the overlapping coherent waves.

[+]

Interference of light: Double-slit Experiment

Double-slit interference experiment (Young's interference experiment), first conducted by Thomas Young in 1801, is a classic demonstration of the phenomenon of interference. This experiment shows that light behaves as a wave when passing through two closely spaced slits with a width comparable to its wavelength.

According to Huygens' principle, each slit acts as a source of secondary waves upon interacting with light wave. Because these new light sources are coherent and in-phase, their superposition forms a characteristic interference pattern of bright and dark fringes on a screen.

Let us consider a point on a screen located at a distance $L$ from two parallel slits, which are illuminated by a coherent light wave with wavelength $\lambda$. The phase relationship of the waves at the observation point depends on the path difference between the rays arriving from each slit: $\Delta\phi = \frac{2\pi d}{\lambda} \sin(\varphi)$.

If the path difference is equal to an integral number of wavelengths the waves will interfere constructively, leading to a bright spot on the screen. The condition for maximum intensity: $$ d\sin\varphi = \pm m \lambda $$

The condition for minimum intensity for observation destructive interference is given by $$ d\sin\varphi = \pm (2m + 1)\frac{\lambda}{2} $$ where $m = 1,2,3...$ order of diffraction, $d$ is the distance between the centres of the slits and $\varphi$ is the angular position of the observation point on the screen relative to the central axis.

To determine how light intensity varies as a function of position on the screen in a double-slit experiment, one must consider the combined effects of interference from the coherent light waves emerging from the two slits and diffraction due to the finite width of each slit. $$I(\varphi) = I_i(\varphi) I_d(\varphi)$$ $$I(\varphi) = I_0\cos^2\left(\frac{\pi d}{\lambda} \sin(\varphi) \right)\text{sinc}^2\left(\frac{\pi a}{\lambda} \sin(\varphi)\right)$$

$\cos^2\left(\frac{\pi d}{\lambda} \sin(\varphi) \right)$ - describes the interference pattern due to the spacing $d$ between the slits, producing alternating bright and dark fringes;
$\text{sinc}^2\left(\frac{\pi a}{\lambda} \sin(\varphi)\right)$ - represents the diffraction envelope due to the finite slit width $a$ modulating the intensity and gradually diminishing the fringe visibility away from the central maximum.

Using the "Visualizer," observe how light diffracts when passing through a single slit. Adjust the wavelength of the beam with the "Wavelength" slider on the left and the aperture size with the "Aperture" slider on the right. This setup allows for easy exploration and observation of the dependencies between wavelength, aperture size, and the resulting diffraction pattern.

[+]

Electrons Interference

The temporal evolution of electrons in space is described by the time-dependent Schrodinger equation: $$i\hbar {\frac {\partial}{\partial t}} \Psi(x,t) = \left( -\frac{\hbar^2}{2m} \Delta + \hat{V}(x) \right)\Psi(x,t)$$ where $\Psi(x,t)$ is the wave function, $\hbar$ is the reduced Planck constant, $m$ is the particle mass (electron), and $\hat{V}(x)$ is the potential. Considir an initial wave packet at $(t = 0)$, extended along the $Oxy$ plane, with its center at $(x_c,y_c)$ and width $x_0$ and $y_0$ along the $x$- and $y$-axis respectively: $$\Psi(x,y,t) = \left(\frac{4}{\pi^2 a_{0x}^2 a_{0y}^2}\right)^{1/4} e^{-\left[\frac{(x-x_c)^2}{a_{0x}^2}+\frac{(y-y_c)^2}{a_{0y}^2} \right]} e^{i[k_{0x}(x - x_c)+k_{0y}(y-y_c)]}$$ where $(k_x,k_y)$are the components of the wave vector $\mathbf(k)$ along the $x$- and $y$-axes. For the simulation of the propagation of a wave packet through a single slit of length $l_s = 2\pi/|k|$, we use a potentiel barrier defined as: $$ V(x,y) = \begin{cases} V_0e^{-|x|}, &\frac{-d}{2} \le x \le \frac{d}{2}, &\forall y\\ 0,&\frac{-l_s}{2} \le y \le \frac{l_s}{2}, &\forall x \end{cases}. $$ where $d$ is the width of the slit along the $x$-axis, and $V_0$ = 100 in the case of an infinite potential barrier.

[+]

Modeling Wave Packet Propagation Through a 2D Slit System

In this section, we can change the profile of the barrier using the following parameters:

The barrier profile: single slit infinite well.

Enter the number of spatial points:
$N_x=$ , $N_y=$
Enter the x-coordinates of the quantum barrier:
$x_{init}=$a.u., $x_{final}=$a.u.
Enter the y-coordinates of the quantum barrier:
$y_{init}=$a.u. $y_{final}=$a.u.
$d=$
$l_s=$

Enter the height of the quantum barrier: $V_{max}=$a.u.
Enter the particle mass: $m=$a.u.

A wave packet is a certain set of waves having different frequencies that describe a formation possessing wave properties, generally limited in time and space. In quantum mechanics, a particle description in the form of wave packets (a set of solitons) is used.

Parameters for the initial wave packet:
$x_c=$, $y_c=$, $x_0=$, $a^y_0=$, $k^x_0=$, $k^y_0=$
Please enter the number of points for the inverse space: $N_{kx}=$, $N_{ky}=$

In this section, wave propagation (the initial state of which is given by the Gaussian profile in the previous section) through the barrier is simulated. In other words, here we can analyze the temporal evolution of the wave packet in the barrier system.

Enter the calculation parameters:

Number of points for time discretization: $N_t=$
Time step: $\Delta t=$
Maximum number of iterations: $N_c^{max}=$
The calculation accuracy based on the Chebyshev expansion: $a_{min}=$
The convergence criteria: $\epsilon=$
The screen position for observing the diffraction: $x=$

Show Fourier decomposition

Show potential energy

Show the screen position

[+]

Some Aspects of Interference Applications

Objective: The phenomenon of interference is widely used in measurement technology due to its high sensitivity to changes in parameters of the system under study. Using the Michelson interferometer as an example, we will explore the use of interference to determine the refractive index or gravitational acceleration from the perspective of classical physics. The application of interference in quantum mechanics will be demonstrated through the use of Cold Atom Gravimeter, which provide highly accurate measurements of gravitational acceleration.

[+]

Interference application: the Michelson interferometer

Wave interference has a broad range of applications, extending from scientific research to practical technologies. In all these cases, the key component is the interferometer - a device that extracts necessary information from interference patterns. Let's focus on one of the types: the Michelson interferometer.
The setup consists of the following components (as shown in Figure (a) below):

A semi-reflective mirror, known as a beam splitter, which divides the beam from a coherent radiation source (such as a laser) into two separate beams.
Beam 1 reflects off Mirror 1 (which can be rotated) and then crosses the beam splitter again before reaching the photodetector (PD).
Beam 2 passes through the beam splitter, reflects off Mirror 2 (which can be moved along the system's axis), and is then reflected by the beam splitter before reaching the photodetector.
The ability to adjust the mirrors allows for control over both the path difference between the beams and the direction of their propagation.

Even the slightest changes in the system - such as adjustments to the length of an arm or variations in the refractive index -cause phase shifts between the optical paths, resulting in different interference patterns:

Constructive interference occurs when the path difference corresponds to a whole number of wavelengths (0, $\lambda$, $2\lambda$…), producing a strong signal.
Destructive interference occurs when the path difference is an odd multiple of half wavelengths ($\lambda/2$, $3\lambda/2$…), resulting in a near-zero signal at the photodetector.
If the two mirrors are strictly perpendicular to each other, the interference pattern appears as concentric circles, known as fringes of equal inclination .
If the mirrors are not perfectly perpendicular, the pattern changes to fringes of equal thickness, forming parallel stripes.

This configuration allows the interferometer to detect and display even minute changes in the optical path, making it highly sensitive to variations within the system.

The Michelson interferometer setup has wide applications in various fields, including:

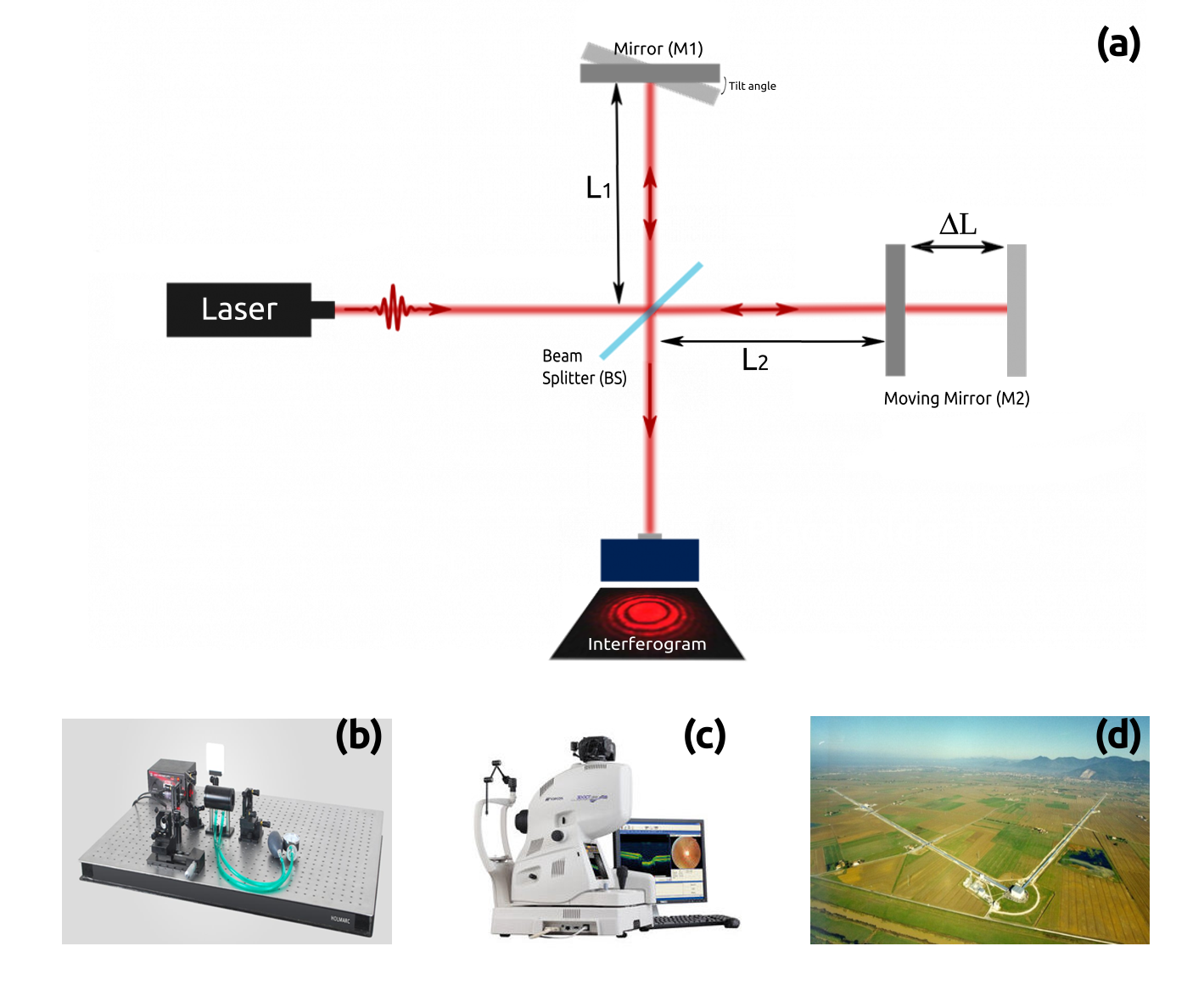
Measurement of light wavelength and refractive index of transparent materials (as shown in figure (b)).

Optical Coherence Tomography (OCT). This non-invasive imaging technique provides high-resolution, cross-sectional images of the retina and optic nerve head, and is commonly used for eye diagnostics in medicine.

Detection of gravitational waves, which plays a key role in modern physics, is being researched at advanced observatories such as LIGO and VIRGO (the photo of the interferometer is shown in figure (c)).

More detailed information can be found in [P. Cheinet],

[+]

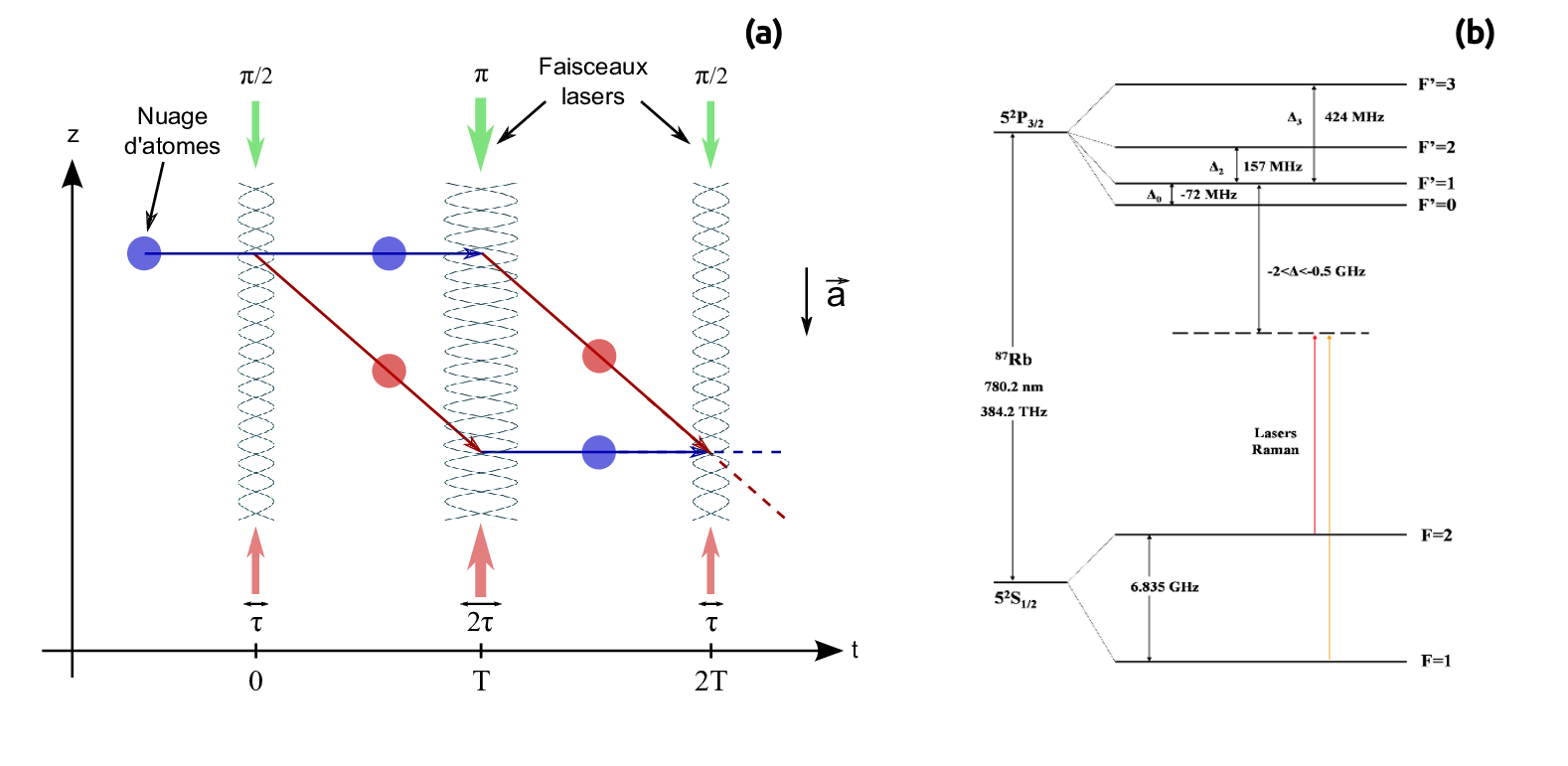
Interference application: Cold Atom Gravimeter

The application of atomic interferometry phenomenon is used in the cold atom gravimeter, which allows for the measurement of gravitational acceleration $g$ with high precision, on the order of $2x10^{-8} g$ per second. First, a few $10^8$ $^{87}Rb$ atoms are captured in a magneto-optical trap. They are cooled down to microKelvin temperatures before being released. During their free fall, they experience a sequence of three laser pulses, that split and recombine the atomic wavepackets. Finally, the phase difference between the two arms of the interferometer, that is proportionnal to $g$, is determined form the measurement of the atomic state at the output of the interferometer.

(a) Principle of a Three-Pulse Atom Interferometer based on simulated Raman transition
(b) the schematic of energy levels of $^{87}Rb$. [M.Langlois],

Two counter-propagating laser beams, whose frequency difference resonates with the energy separation between the two hyperfine levels $|a⟩ = |5S_{\frac{1}{2}}, F = 1⟩$ and $|b⟩ = |5S_{\frac{1}{2}}, F = 2⟩$,
induce a transition between these two levels, that accompanied by a momentum transfer of $ \hbar(k_1 - k_2) = \hbar k_{eff}$ from the two beams, allowing for the spatial separation of the two states.

After being selected in the state $|{a}\rangle$, the $^{87}Rb$ atoms will undergo, in order: a $\frac {\pi} 2$ transition (splitting), a $\pi$ transition (mirror), and a $\frac {\pi} 2$ transition (recombination).

To determine $g$, we need to know the probability of finding an atom in one of the states:

$$P=\frac {N_{|{a}\rangle}}{N_{|{a}\rangle}+ N_{|{b}\rangle}}$$

In practice, due to the Doppler effect, the resonance frequency of the Raman process depends on velocity. As the atoms are in free fall, it is necessary to sweep the frequency difference between the Raman laser beams to satisfy the resonance condition for each pulse. Thus, the phase shift $\alpha T^2$ is added to the gravitational phase shift (where $\alpha/2\pi$ is the frequency sweep rate). If $T$ is total time between the first and last laser pulses and $\tau$ is the time between each consecutive pulse, the phase shift can be rewritten as: $$\Delta \phi = (k_\text{eff}g-a)(T+2\tau)(T+4\tau/\pi)$$ The fringes are recorded by varying $\alpha$ for each measurement. When the Doppler effect is perfectly compensated, regardless of the value of $T$, the total phase shift $\Delta \phi$ becomes zero. The corresponding dark fringe associated with its sweep rate $\alpha_0$ allows to determine the value of $g$: $$ g = \frac{\alpha_0}{k_{eff}}$$

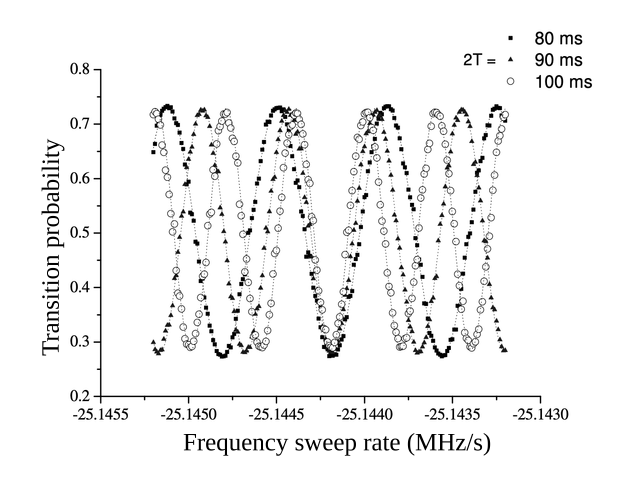
Interference fringes. The transition probability is measured as a function of the frequency ramp applied to the Raman beams. The fringe that remains dark, regardless of the interrogation time, is the one for which the ramp precisely compensates for the Doppler effect, thereby allowing the measurement of $g$. [F. PEREIRA DOS SANTOS].

From this data, we obtain $\alpha_0/2\pi = 25.1442 MHz.s^{-1}$;
Using the formula for $g$ and the value of $k_{eff} = 2 \pi * 2.56330737276 * 10^6 $ for Rubidium-87 atoms, we calculate $g = 9.809280099298581 \frac{m}{s^2}$

More detailed information can be found in [P. Cheinet], [SYRTE].

Open notebook

v.1.2 [15.06.2023-15.07.2024]. Full-stack programming and site design by M. Sosnova (mariya.v.sosnova@gmail.com)