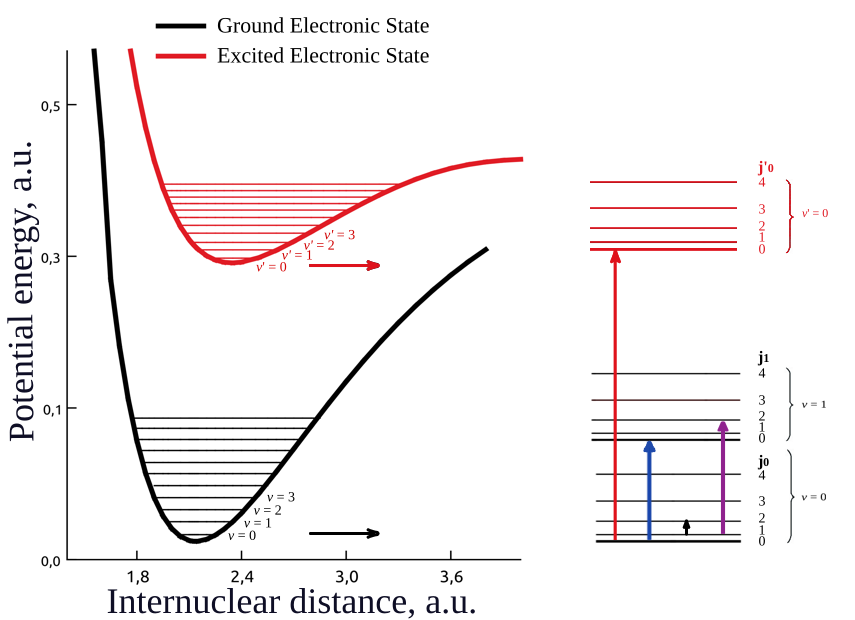
The potential energy diagram for CO (Molpro 2020.1) and a schematic representation of molecular energy levels with the types of possible transitions: red arrows denote transitions involving a change in the electronic state, blue indicate transitions between different vibrational states, black represent transitions involving only rotational energy levels, violet correspond rotational-vibrational transitions (see left figure).
The typical energy interval for elecronic, vibrational and rotational motion:
| Motion | Energy interval |
|---|---|
| Electronic | Visible / UV region: 10000 - 50000 cm \(^{-1}\) |
| Vibrational | Near Infrared region: 2000 - 4000 cm \(^{-1}\) |
| Rotational | Microwave/Far-Infrared region: 1 - 20 cm \(^{-1}\) |
The stationary state of a molecule is well approximated by the sum of its electronic \(E_e\), vibrational \(E_v\), rotational \(E_r\) energies ( \( E_m = E_e + E_v + E_r \) ) and by product of corresponding wave functions.
To understand the fundamental principles of molecular spectroscopy, the experimental rotational-vibrational spectrum of carbon monoxide (see below) will be analyzed. CO is diatomic heteronuclear molecule with a permanent dipole moment, that changes during vibration. So, the molecule can be approximated as a rigid rotator with a fixed bond length at equilibrium.
To compute the vibrational-rotational energy levels and wavefunctions of a diatomic molecule, we solve the time-independent Schrödinger equation: $$H \Psi(r) = E\Psi(r)$$ where the Hamiltonian \(H\) is the sum of kinetic energy \(T\) and the effective potential energy \(V_\mathrm{eff}(r)\) which takes into account the rotational energy contribution: $$ V_\mathrm{eff}(r) = V(r) + \frac{\hbar^2}{2\mu r^2}(j(j+1)-\Lambda^2) $$ where \(j\) is the total angular momentum quantum number, \(\Lambda\) is the projection of the electronic angular momentum onto the internuclear axis (for CO, \(\Lambda = 0\)), and \(\mu \) is the reduced mass of the diatomic molecule, given by $$\mu = \frac{m_1m_2}{m_1 + m_2}.$$ where \(m_1\) and \(m_2\) are the masses of the two atoms that form the molecule.
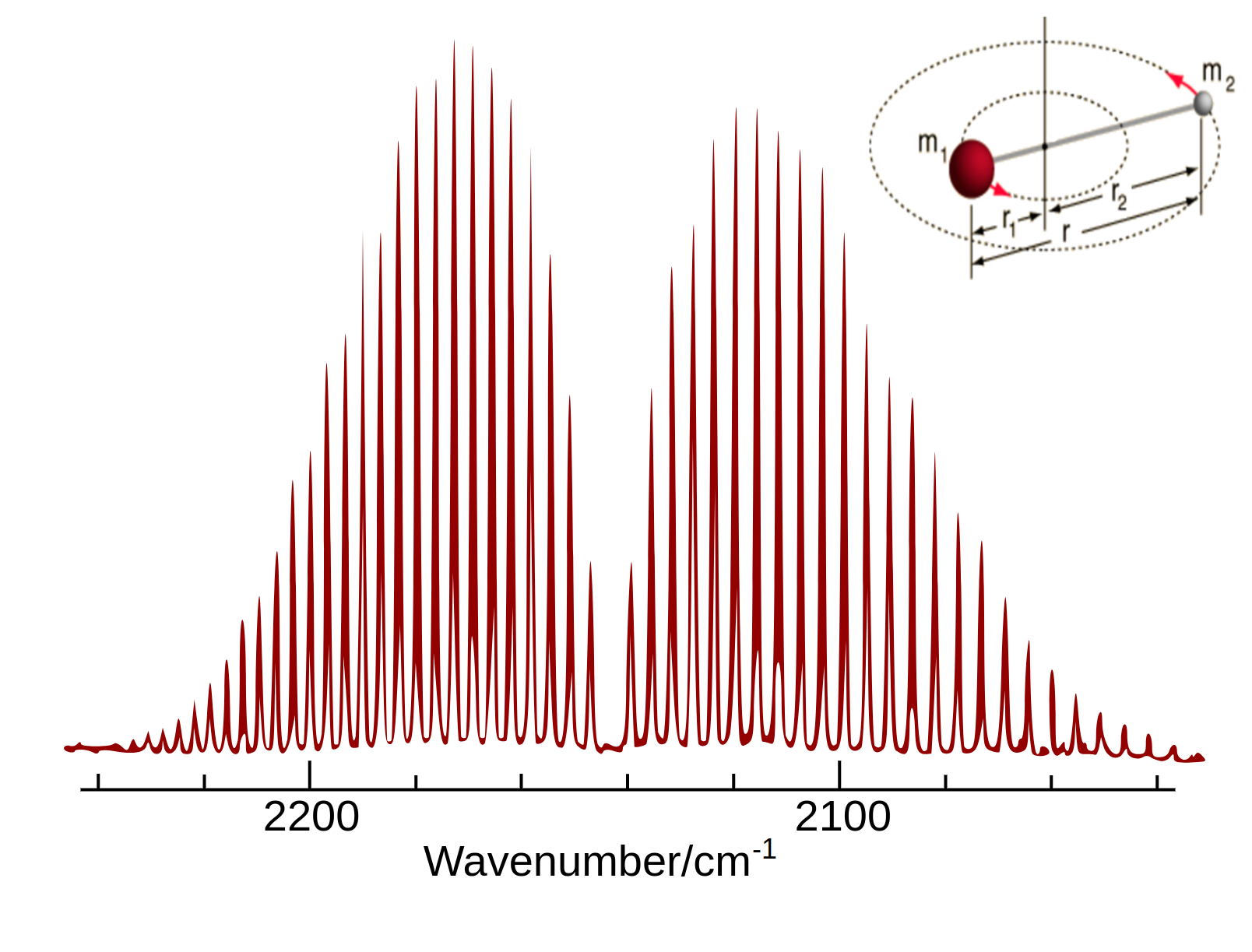
Experimental rotational-vibrational absorption spectrum of the carbon monoxide obtained by Fourier Transform Infrared (FTIR) spectroscopy method.
Atomic units are used, where the unit of charge is \(e = 1\) (\(1.602176634×10^{−19}\)C); the unit of mass \(m_e = 1\) is defined as the mass of the electron (\(9.1093837139(28)×10^{−31} \)kg); the unit of action \(\hbar = 1\) - reduced Planck constant (\(1.054571817...×10^{−34}\) J⋅s); the unit of length \(a_0 = 1\) - Bohr radius (\(a_0 = 4\pi\epsilon\hbar^2 / m_e e^2 = 0.529×10^{−10}\)m); the unit of energy \(E_H = 1\) - Hartree energy (\(E_H = \hbar^2/m_e a_0^2 = 4.359×10^{-18}\) J = 27.211 eV).
The masses in the boxes below are given in daltons (Da) or unified atomic mass units (u). The unified atomic mass unit should not be confused with atomic unit of mass (\(m_e\)). 1u= 1822.88848 \(m_e\).
To describe the anharmonic interaction between the atoms in a diatomic molecule the Morse potential is used: $$V(r) = D_e \left( 1 - e^{-\alpha(r - r_e)}\right)^2$$ where \(D_e\) is the dissociation energy, \(\alpha\) determines the width of the potential well, and \(r_e\) is the equilibrium bond length.
For a diatomic molecule the equilibrium (for \(v = 0 \)) rotational constant \(B_e\) can be approximated using: $$ B_e = \frac{\hbar^2}{2 I c} , $$ where \( I = \mu r^2\) is the moment of inertia, with \(r\) being the equlibrium bond length.
The rotational constant for a specific vibrational state (\(B_v\)) takes into account the influence of the molecule's vibrational state on its rotational energy due to anharmonic effects and changes in the bond length \(r\) that occur as the molecule vibrates: $$ B_v=\int dr u_{v,0}^*(r)\left(\frac{\hbar^2}{2\mu r^2}\right)u_{v,0}(r), $$ where, \(u_{v,0}(r)\) is the vibrational wavefunction for the \(v\)-th vibrational state, describing the probability of finding a molecule at a certain bond length \(r\), the vibrational state \(v\) and \(\frac{\hbar^2}{2\mu r^2}\) represents the rotational energy contribution for the molecule.
For a diatomic molecule, the vibrational energy is given by: $$ E_v = \left( v + \frac{1}{2}\right)h \nu, $$ where \(v = 0, 1, 2, ...\) is the vibrational quantum number, \(\nu\) ist the vibrational frequency of the molecule.
The rotational energy for a rigid diatomic rotor is quantized: $$ E_j = B_vj(j + 1), $$ where \(j\) is rotational quantum number (0, 1, 2, ..), \(B_v\) - the rotational constant with a correction factor introduced to account for the distortion of the molecule due to rotation.
For rotational and vibrational transitions the transition dipole moment, expressed as: $$ \mathcal{I}_{v'j',vj}=\int dru^*_{v'j'}(r)D(r)u_{vj}(r) $$ where:
- \(u_{vj}(r)\) are the wave functions for a specific quantum state characterized by the vibrational quantum number \(v\) and rotational quantum number \(j\) .
- \(D(r)\) is the dipole moment function, which describes how the molecular dipole moment varies with internuclear distance \(r\). This function typically depends on the molecular structure.
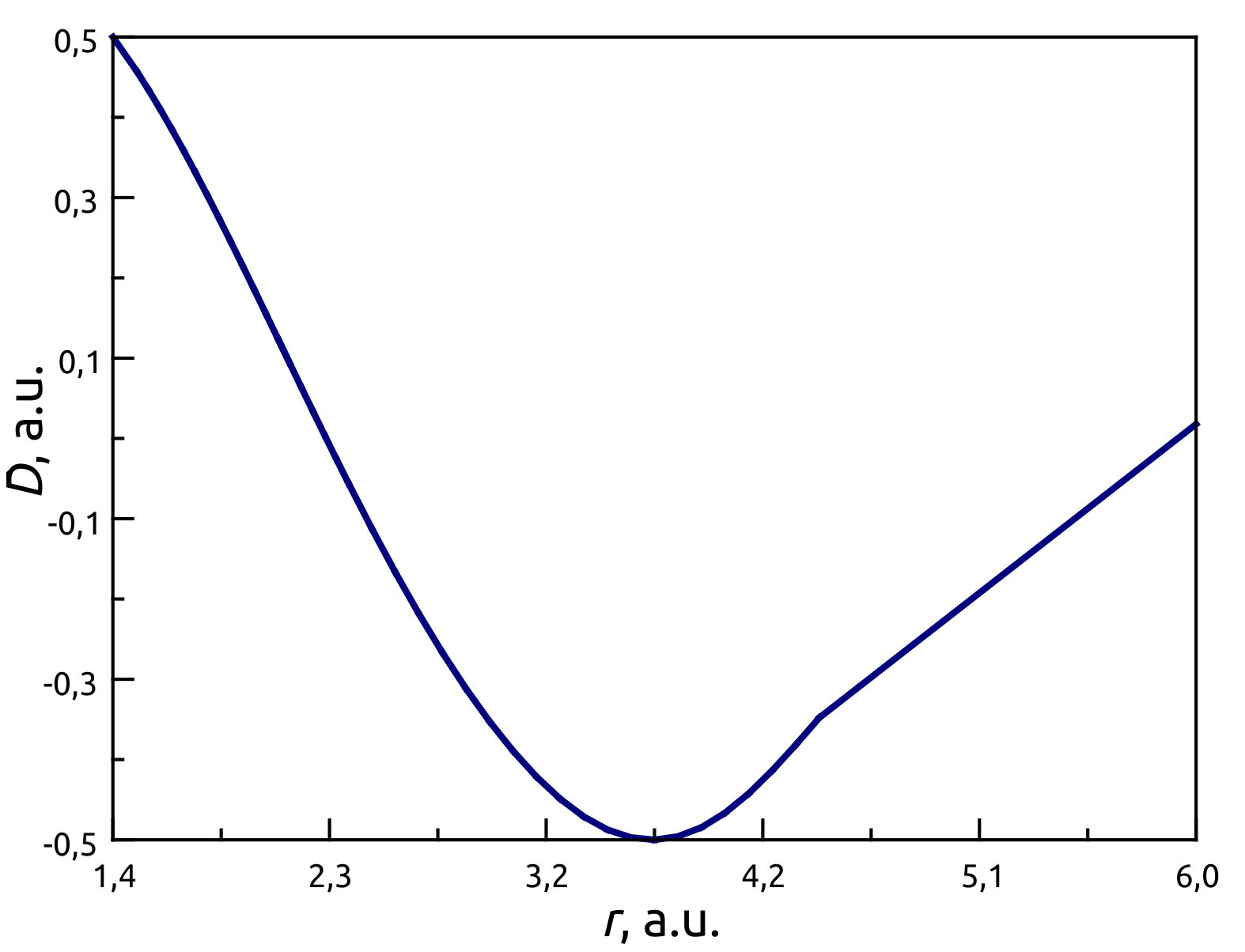
To determine the dipole moment \(D(r)\) for CO in ground state we use a software package for ab initio quantum chemistry calculations MOLPRO .
- Vibrational Transitions: \(\Delta v = \pm 1, \pm 2, ...\) The most intense transitions occur for fundamental transitions (\(\Delta v = \pm 1\)).
- Rotational Transitions: Due to the interaction of the dipole moment with rotational motion, allowed transitions must follow: \(\Delta J = \pm 1\).
- The molecule must have a changing dipole moment during vibration for the transition to be allowed.
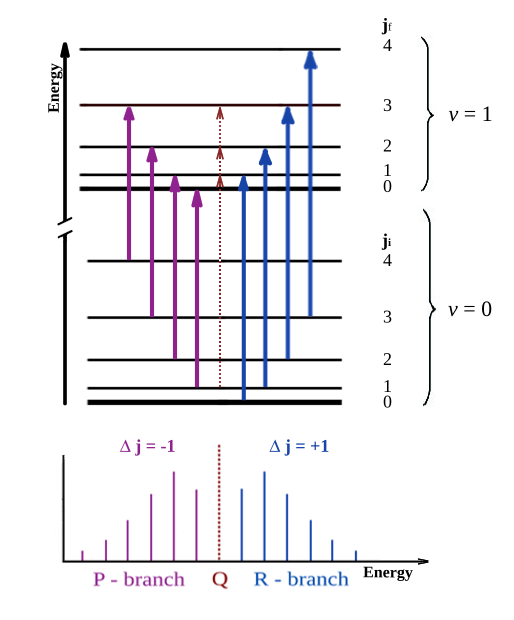
For modeling the infrared spectrum of the \( v = 1 ← 0\) transition of CO molecule at room temperature, use the following expressions for the transition rates:
The intensity of a rotational-vibrational transition in molecule between two level for R - branch describe by expression:\(\Psi_{v,j,m}\) and \(\Psi_{v',j',m'}\) are the wavefunctions of the initial and final states, respectively, with the quantum numbers \(v = 0\), \(v' = 1\) for vibrational states and \(j' = j \pm 1\) for rotational states.
The rotational-vibrational spectra provide critical information about various molecular properties, such as molecular structure (e.g., bond lengths), molecular dynamics (e.g., bond strengths), energy levels and transitions etc. This makes infrared spectroscopy an essential tool in molecular physics, spectroscopy, and applied fields such as environmental monitoring, material analysis, and chemical identification.
THE PROJECT IS SUPPORTED BY





