This notebook introduces the fundamental concepts of quantum computation, covering qubits and the physical systems necessary to their practical implementation. Quantum computing requires maintaining quantum effects in large systems, which presents a challenge even with current materials or quantum circuits developed through modern manufacturing techniques.
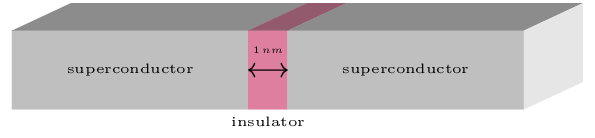
With the use of superconductivity one can manufacture highly non-dissipative quantum systems displaying non-linear inductance called Josephson junctions, which constitute a physical realization of qubits used in quantum computing. Both the non-linearity and non-dissipativeness are of the utmost importance for the control and maintenance of the quantum states. Using them, one can perform linear algebra on superposition states using quantum mechanical means, in order to perform computation using specially designed quantum algorithms (which are very much distinct from the classical algorithms used in classical computers) or to perform simulations of quantum mechanical systems.
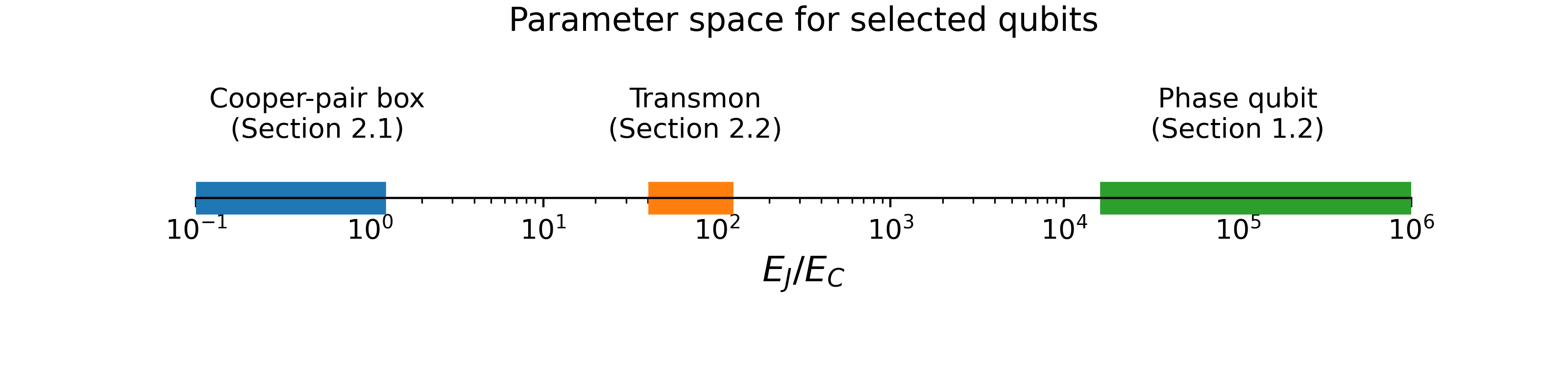
The next figure on the left presents the dependence of energies of lowest laying states of the Josephson junction as a function of the ratio between the tunneling energy \(E_J\) and the charging energy \(E_C\) and the Cooper-pair occupation offset \(n_g\). For some selected values of \(E_J/E_C = \) we can observe how the energy levels evolve with changing coupling parameters. With increasing the value of \(E_J/E_C\) the distances between energy levels become more pronounced and the system loses the dependence on the parameter \(n_g\). Where \(n_{g}\) changes in interval \((-1;1)\) and \(N=\) .
The right figure demonstrates how absolute anharmonicity \(\alpha\) changes as a function of the parameter ratio \(E_J/E_C\).
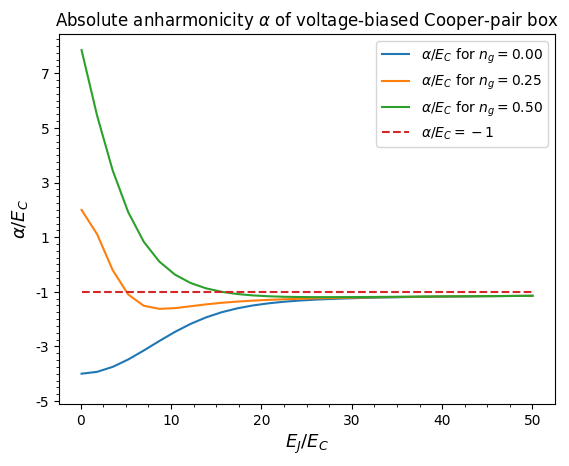
From those two graphs one can deduce that the two lowest states of the Josephson junction form a two-dimensional unitary space, representing a qubit. By arranging multiple Josephson junctions on an integrated circuit and interconnecting them, one can manipulate the ensemble's state, facilitating computations before the quantum state decoheres due to inevitable interactions with the macroscopic classical environment.
- Harmonic and anharmonic potentials: will discuss the harmonc and anharmonic nature of quantum mechanical systems.
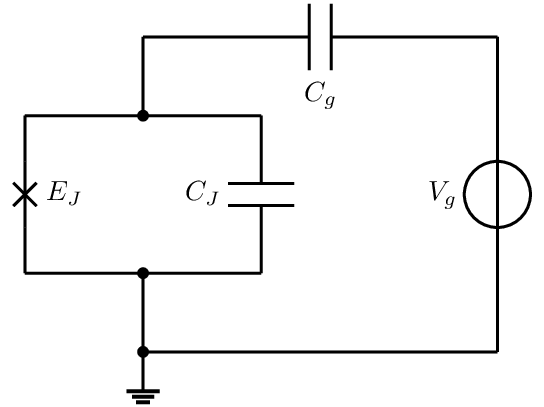
- Physical realisations of Josephson junctions: will present one type of Josephson junction - a charge qubit and discussed two regimes of this system: voltage-biased Cooper-pair box and transmon qubit.